Zorn's lemma

Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:

Suppose a partially ordered set P has the property that every chain (i.e. totally ordered subset) has an upper bound in P. Then the set P contains at least one maximal element.

It is named after the mathematicians Max Zorn and Kazimierz Kuratowski.

The terms are defined as follows. Suppose (P,≤) is a partially ordered set. A subset T is totally ordered if for any s, t in T we have s ≤ t or t ≤ s. Such a set T has an upper bound u in P if t ≤ u for all t in T. Note that u is an element of P but need not be an element of T. An element m of P is called a maximal element if there is no element x in P for which m < x.

Note that P is not required to be non-empty. However, the empty set is a chain (trivially), hence is required to have an upper bound, thus exhibiting at least one element of P. An equivalent formulation of the lemma is therefore:

Suppose a non-empty partially ordered set P has the property that every non-empty chain has an upper bound in P. Then the set P contains at least one maximal element.

The distinction may seem subtle, but proofs involving Zorn's lemma often involve taking a union of some sort to produce an upper bound. The case of an empty chain, hence empty union is a boundary case that is easily overlooked.

Zorn's lemma is equivalent to the well-ordering theorem and the axiom of choice, in the sense that any one of them, together with the Zermelo–Fraenkel axioms of set theory, is sufficient to prove the others. It occurs in the proofs of several theorems of crucial importance, for instance the Hahn–Banach theorem in functional analysis, the theorem that every vector space has a basis, Tychonoff's theorem in topology stating that every product of compact spaces is compact, and the theorems in abstract algebra that every nonzero ring has a maximal ideal and that every field has an algebraic closure.

An example application

We will go over a typical application of Zorn's lemma: the proof that every nontrivial ring R with unity contains a maximal ideal. The set P here consists of all (two-sided) ideals in R except R itself, which is not empty since it contains at least the trivial ideal {0}. This set is partially ordered by set inclusion. We are done if we can find a maximal element in P. The ideal R was excluded because maximal ideals by definition are not equal to R.

We want to apply Zorn's lemma, and so we take a non-empty totally ordered subset T of P and have to show that T has an upper bound, i.e. that there exists an ideal I ⊆ R which is bigger than all members of T but still smaller than R (otherwise it would not be in P). We take I to be the union of all the ideals in T. Because T contains at least one element, and that element contains at least 0, the union I contains at least 0 and is not empty. Now to prove that I is an ideal: if a and b are elements of I, then there exist two ideals J, K ∈ T such that a is an element of J and b is an element of K. Since T is totally ordered, we know that J ⊆ K or K ⊆ J. In the first case, both a and b are members of the ideal K, therefore their sum a + b is a member of K, which shows that a + b is a member of I. In the second case, both a and b are members of the ideal J, and we conclude similarly that a + b ∈ I. Furthermore, if r ∈ R, then ar and ra are elements of J and hence elements of I. We have shown that I is an ideal in R.

Now comes the heart of the proof: why is I smaller than R? The crucial observation is that an ideal is equal to R if and only if it contains 1. (It is clear that if it is equal to R, then it must contain 1; on the other hand, if it contains 1 and r is an arbitrary element of R, then r1 = r is an element of the ideal, and so the ideal is equal to R.) So, if I were equal to R, then it would contain 1, and that means one of the members of T would contain 1 and would thus be equal to R – but we explicitly excluded R from P.

The condition of Zorn's lemma has been checked, and we thus get a maximal element in P, in other words a maximal ideal in R.

Note that the proof depends on the fact that our ring R has a multiplicative unit 1. Without this, the proof wouldn't work and indeed the statement would be false. For example, the ring with 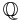as additive group and trivial multiplication (i. e. 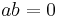for all 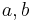) has no maximal ideal (and of course no 1): Its ideals are precisely the additive subgroups. The factor group 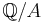by a proper subgroup is a divisible group, hence certainly not finitely generated, hence has a proper non-trivial subgroup, which gives rise to a subgroup and ideal containing .

Sketch of the proof of Zorn's lemma (from the axiom of choice)

A sketch of the proof of Zorn's lemma follows. Suppose the lemma is false. Then there exists a partially ordered set, or poset, P such that every totally ordered subset has an upper bound, and every element has a bigger one. For every totally ordered subset T we may then define a bigger element b(T), because T has an upper bound, and that upper bound has a bigger element. To actually define the function b, we need to employ the axiom of choice.

Using the function b, we are going to define elements a₀ < a₁ < a₂ < a₃ < ... in P. This sequence is really long: the indices are not just the natural numbers, but all ordinals. In fact, the sequence is too long for the set P (see Hartogs number); there are too many ordinals, more than there are elements in any set, and the set P will be exhausted before long and then we will run into the desired contradiction.

The a_i are defined by transfinite recursion: we pick a₀ in P arbitrary (this is possible, since P contains an upper bound for the empty set and is thus not empty) and for any other ordinal w we set a_w = b({a_v: v < w}). Because the a_v are totally ordered, this is a well-founded definition.

This proof shows that actually a slightly stronger version of Zorn's lemma is true:

If P is a poset in which every well-ordered subset has an upper bound, and if x is any element of P, then P has a maximal element that is greater than or equal to x. That is, there is a maximal element which is comparable to x.

History

The Hausdorff maximal principle is an early statement similar to Zorn's lemma.

K. Kuratowski proved in 1922^[1] a version of the lemma close to its modern formulation (it applied to sets ordered by inclusion and closed under unions of well-ordered chains). Essentially the same formulation (weakened by using arbitrary chains, not just well-ordered) was independently given by Max Zorn in 1935,^[2] who proposed it as a new axiom of set theory replacing the well-ordering theorem, exhibited some of its applications in algebra, and promised to show its equivalence with the axiom of choice in another paper, which never appeared.

The name "Zorn's lemma" appears to be due to John Tukey, who used it in his book Convergence and Uniformity in Topology in 1940. Bourbaki's Théorie des Ensembles of 1939 refers to a similar maximal principle as "le théorème de Zorn".^[3] The name "Kuratowski–Zorn lemma" prevails in Poland and Russia.

Equivalent forms of Zorn's lemma

Zorn's lemma is equivalent (in ZF) to three main results:

1. Hausdorff maximal principle
2. Axiom of choice
3. Well-ordering theorem.

Moreover, Zorn's lemma (or one of its equivalent forms) implies some major results in other mathematical areas. For example,

1. Banach's extension theorem which is used to prove one of the most fundamental results in functional analysis, the Hahn–Banach theorem
2. Every vector space has a Hamel basis, a result from linear algebra
3. Every commutative unital ring has a maximal ideal, a result from ring theory
4. Tychonoff's theorem in topology.

In this sense, we see how Zorn's lemma can be seen as a powerful tool, especially in the sense of unified mathematics.

References

• Ciesielski, Krzysztof (1997). Set Theory for the Working Mathematician. Cambridge University Press. ISBN 0-521-59465-0. 
• Campbell, Paul J. (February 1978). "The Origin of ‘Zorn's Lemma’". Historia Mathematica 5 (1): 77–89. doi:10.1016/0315-0860(78)90136-2. 

External links

• Zorn's Lemma at ProvenMath contains a formal proof down to the finest detail of the equivalence of the axiom of choice and Zorn's Lemma.
• Zorn's Lemma at Metamath is another formal proof. (Unicode version for recent browsers.)